A verdadeira história da Fórmula de Bhaskara

[♀]Matemática na Veia 2007-2016 O Blog do Estudante Inteligente

Relatos de erros e correções em relação ao português serão bem vindos e podem ser esclarecidos através do RH - Sugestões e Reclamações.

A FÓRMULA DE BASKARA

As referências mais antigas sobre a resolução de problemas envolvendo equações do segundo grau foram encontradas em textos babilônicos escritos há cerca de 4 000 anos atrás.

Embora os babilônios tivessem conseguido resolver muitos problemas matemáticos envolvendo equações quadráticas, cada problema era resolvido para aquele caso particular e sua solução era uma espécie de receita prática, que não especificava nem a sua fórmula geral, nem o modo como a solução havia sido obtida. Embora essas "receitas" , quando aplicadas a problemas do segundo grau, conduzissem de forma natural à dedução da fórmula de Bhaskara, os antigos babilônios não chegaram a generalizar tais "receitas".

Na Grécia, as equações de segundo grau eram resolvidas por meio de construções geométricas como iremos ver num exercício que ilustra o método geométrico utilizado por Euclides para achar a solução da equação x² = s² - sx.

No século XII D.C.,Bhaskara [1114-1185], em duas das suas obras, apresenta e resolve diversos problemas do segundo grau. Antes de Bhaskara, no princípio do século IX D.C., o matemático árabe Al-Kowarismi, influenciado pela álgebra geométrica dos gregos, resolveu, metodicamente, as equações do segundo grau, chegando à fórmula do modo descrito a seguir. 

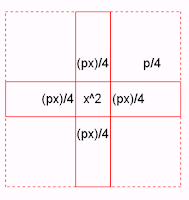
Al-Kowarismi interpretava, geometricamente, o lado esquerdo da equação x² + px = q como sendo uma cruz constituída por um quadrado de lado x e por quatro retângulos de lados p/4 e x. Então, como mostra a figura abaixo, "completava" esta cruz com os quatros quadrados pontilhados de lado p/4, para obter um "quadrado perfeito" de lado x + p/2..

 

Empregando este artifício geométrico, Al-Kowarismi conseguiu demonstrar que adicionando 4 vezes p²/16 , a soma das áreas dos quatros quadrados de lado p/4 , ao lado esquerdo da equação x² + px = q, obtinha-se (x + p/2)², que é a área do quadrado de lado x + p/2 , isto é,x² + px + 4 p²/16 = (x + p/2)² .

Portanto, a equação x² + px = q poderia ser escrita como (x + p/2)² = q + p²/4 implicando que x = -p/2 ±  , que é a fórmula de Bhaskara.

A descoberta de que um trinômio do segundo grau tem para imagem uma parábola, remonta à Antiguidade. As primeiras referências a respeito encontram-se nos trabalhos do matemático grego Menaecamus [ 375-325 A.C. ], que obteve a parábola seccionando um cone circular reto por um plano não paralelo à base. Pode-se provar que a curva assim obtida é a imagem de uma equação do tipo y = ax², como mostra a figura ao lado.

Veja também as Biografias de Matemáticos famosos disponíveis aqui no blog.

Em breve mais atualizações, aguarde.

Se você quer cooperar com dicas, programas, artigos. Fique a vontade, e mande um e-mail para caco36@ibest.com.br ,ou comente aqui mesmo, por enquanto é só. Agradeço antecipadamente, comentários, dicas, criticas e sugestões.

Observação:

- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.

- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .

Assine aqui, o Feed do Matemática Na Veia , e receba por e-mail os artigos do blog. Fique por dentro das novidades, e curiosidades da matemática.

REFERÊNCIA:

http://www.im.ufrj.br/dmm/

Share on Google Plus

Sobre a Autor:

Antonio Blogueiro desde 2007, gaúcho, gosta muito de ler, e é totalmente viciado em internet. Comecei blogar em 2005, e criei o Matemática na Veia no inicio de 2007. Sou formado em licenciatura Plena em Matemática pela UFPEL. Servidor Público,e fanático pela Web.