A importância da análise combinatória na matemática é incontestável, apesar de ser um tema que envolve muitas dificuldades em relação à formulação e, principalmente, no que diz respeito à interpretação dos seus enunciados. Podemos concluir que, não basta apenas sabermos as propriedades e decorarmos as fórmulas, temos que interpretar cada segmento do problema proposto, ou seja, temos que dividir o problema para tornar a interpretação mais fácil.
É claro que nossa natureza é imediatista, pois somos criados assim. Queremos tudo pronto para ontem, o que é um “veneno”, quando se trata de interpretarmos problemas matemáticos. Seguindo esta linha de raciocínio, propomos que você leia o conteúdo completamente, para não perder detalhes muito importantes, e que desenvolva todos os exercícios disponíveis, e se mesmo assim, surgirem dúvidas referentes aos mesmos, faça suas perguntas aqui no blog.
Para começarmos um novo conteúdo vamos recordar rapidinho o que aprendemos no último artigo. Aprendemos que “Binomiais complementares” são dois números binomiais que apresentam o mesmo numerador e que a soma de suas classes é igual ao denominador.
Os dados são representados por números consecutivos, de forma que seja possível descobrir seu complementar a cada jogada feita.

Observação: Nunca esqueça que classe é o denominador, ou seja, o número de baixo de um coeficiente binomial. E que coeficiente binomial é um número binomial. Agora que já recordamos o significado de “Binomiais complementares”, vamos começar um novo conteúdo.
Dois números binomiais de mesmo numerador são consecutivos se suas classes são números consecutivos.
Por exemplo, são consecutivos os seguintes binomiais:
Supondo satisfeitas as condições de existência de dois binomiais consecutivos, é válida a relação a seguir, denominada relação de Stifel, também conhecida como regra de Pascal é representada pela seguinte igualdade:

(Michael Stifel, matemático alemão, 1486 - 1567). Foi considerado o maior algebrista da Alemanha do séc. XVI.
A relação de Stifel, como se pode observar expressa a soma de dois números binomiais consecutivos em função de um único binomial.
Por exemplo:
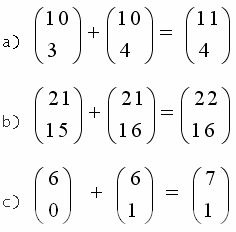
Observe os exemplos a seguir, em que utilizamos a relação de Stifel para a resolução de equações que envolvem os números binomiais.
Resolva as equações seguintes:
Resolução:
Aplicando a relação de Stifel duas vezes no segundo membro da igualdade, obtemos:
Resolução:
Neste caso vamos aplicar a relação de Stifel para decompor
Resolução:
Substituindo o binomial 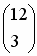 pelo seu complementar, teremos:
pelo seu complementar, teremos:
 E3-Exercícios:
E3-Exercícios:
1- Dentre as igualdades, identifique as verdadeiras.
a)V b)V c)F d)F e)F f)V g)F
2 – Escreva cada uma das expressões em função de um único número binomial.
Gabarito:
 3 – Resolva as equações:
3 – Resolva as equações:
Gabarito:
a) S={8;9} b) S={7;11} c) S={41;18} d) S={1/2;3}
Por enquanto ficamos por aqui. Em breve mais atualizações, aguarde!
Se você é aluno, professor, ou simplesmente um apaixonado pela matemática, e gostaria de cooperar com dicas, indicar algum blog legal de matemática, ou que seja relacionado à educação, programas legais que conhece, artigos, trabalhos de escola. Mande um e-mail para caco36@ibest.com.br,ou comente aqui mesmo. Agradeço sua cooperação, comentários, dicas, críticas e sugestões.
Observação:
- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.
- Crie um ponto de restauração no Windows, antes de instalar qualquer programa, ou arquivo.
REFERÊNCIAS
BACHX, A. de; POPPE, L. M. B.; TAVARES; RAYMUNDO N. O. – Prelúdio à Análise Combinatória. Companhia Editora Nacional. 1975
CARVALHO, P. C. P; LIMA, E. L.; MORGADO, A. C; WAGNER, E. – A Matemática do Ensino Médio. Vol. 2. Coleção do Professor de Matemática. Sociedade Brasileira de Matemática. 1998
CARVALHO, J. B. P; CARVALHO, P. C. P; FERNANDEZ, P; MORGADO, A. C de O. – Análise Combinatória e Probabilidade. Coleção do Professor de Matemática.
 Sobre a Autor:
Sobre a Autor:
Antonio
Blogueiro desde 2007, gaúcho, gosta muito de ler, e é totalmente viciado em internet.
Comecei blogar em 2005, e criei o Matemática na Veia no inicio de 2007.
Sou formado em licenciatura Plena em Matemática pela UFPEL. Servidor Público,e fanático pela Web.



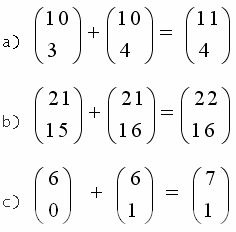






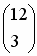 pelo seu complementar, teremos:
pelo seu complementar, teremos: 
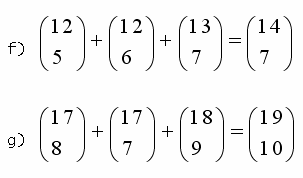

 Sobre a Autor:
Sobre a Autor:














Olá, sou Professor de Matemática e gostei bastante desse blog, tem um visual legal. Também tenho um blog de matemática, o endereço é http://eclesio.zip.net
ResponderExcluirQue bom um blog de matemática, estou seguindo você, e vou adicionar seu blog ao meu, acho importante estarmos perto de soluções, gostei do blog, abraços.
ResponderExcluirMauro
Sei a resposta, não entendo o porque, nem imagino...
ResponderExcluir"Uma escola oferece cursos para a aprendizagem de apenas cinco idiomas. Sabendo que cada professor dessa escola ministra aulas de exatamente dois idiomas e que, para cada dois idiomas, há um único professor que ministra aulas desses dois idiomas, é correto afirmar que o número de professores dessa escola é:
A resposta é 10".
Valeu Eclésio! Vou dar uma passada no teu blog. Derrepente trocamos uma idéias.
ResponderExcluirAbraços.
Tudo bem Mauro? Legal esta pergunta, pois pode ser generalizada da seguinte forma.
ResponderExcluirn(n-1)/2 onde n é o número de idiomas oferecidos pelo curso.
Observe que se for
n=2 teremos 1 professor.
n=3 teremos 3 professores
n=4 teremos 6 professores
n=5 teremos 10 professores
.
.
.
E assim indefinitivamente.
Se você já ouviu falar sobre números triangulares deve ter percebido que a sequência 1,3,6,10,15,21... é uma sequência de números triangulares.
Também pode ser usado a ideia de combinações simples.
Fazendo k!/p!(k-p)! onde k é o número total de idiomas, e p é um subconjunto de k.
Dê uma olhada no tópico combinações simples para entender melhor.
Se precisar de mais detalhes posso criar um desenho para visualizar melhor o problema
Abraços.
Meu seu blog é espetacular, show, not°10 desejo muito sucesso em sua caminhada e objetivo no seu Hiper blog
ResponderExcluirUm grande abraço e tudo de bom
http://maximumforma.blogspot.com/
Valeu Rodrigo, e Util! Um abração para vocês...
ResponderExcluirolá, sou Milena,
ResponderExcluirPoderiam responder esta questão?
Quanto é a – b ?
uma reta corta uma outra que está na horizontal;
em cima dois angulos: 5x+70 e a;
em baixo dois angulos: b (que é oposto e igual a 5x+70 e "a" (oposto de a).
valeu; favor mande a resposta para o email rrss78@bol.com.br
nao consigo entender nada ... preciso saber quando for (7 ) = (7)
ResponderExcluir(x) (3) nao entendo como fazer ...qual me explica por favor ...?
nao consigo entender nada ... preciso saber quando for (7 ) = (7)
ResponderExcluir(x) (3) nao entendo como fazer ...qual me explica por favor
...?
gostei, gostaria de mais exemplo, como somatorio de coeficientes
ResponderExcluirnão entendi pqe a questão 2 (d) deu esse resultado
ResponderExcluirThank you for the good writeup. It in fact was a amusement account it.
ResponderExcluirLook advanced to more added agreeable from you!
By the way, how could we communicate?
My page download pokemon x and y