O QUE É FATORIAL?
Fatorial é uma expressão que tem por função determinar um número sucessor com ajuda do anterior ou anteriores. Este procedimento é chamado de recursividade.
Durante o desenvolvimento da análise combinatória muitos matemáticos adotaram diferentes simbologias para denominar as mesmas operações. O símbolo π (n) foi instituído por Gauss (1777-1855) para representar o produto dos n primeiros números naturais, A. M. Legendre (Paris, 1811) usava o símbolo; a notação ()n(1+Γn n usada por outros autores. A Arbogast (Strasburgo, 1800) deve-se a denominação fatorial. )
Já a notação que conhecemos n!(fatorial de n ) , foi introduzida por Christian Kramp em (Colônia,1808) em seu livro "Elements d'arithmétique universelle"
Observação: O zero não entra nesta definição, pois se multiplicarmos todo o produto de n até 1 por zero teremos zero como resultado. Logo o fatorial de n pode ser definido como:
Para todo

, n!= n(n-1)(n-2)...1
Define-se ainda que :
Para n=0 temos que n!=1
Para n=1 temos que n!=1
Exemplos I:
a)
0! = 1
1! = 1
2! = 2.1=2
3! = 3.2.1=6
4! = 4.3.2.1=24
5! = 5.4.3.2.1=120
.
.
.
n!= n(n-1)(n-2)...1
b) Também é importante destacar, que o desenvolvimento de um fatorial pode ser representado utilizando um outro fatorial menor. Nesse caso, trucamos(quebramos) o desenvolvimento de n! num fator qualquer e utilizamos novamente o simbolo”!”.
Exemplos II:
a) 3!=3.2.1=6 desenvolvendo todo o produto sem truncar nenhum fator.
3!=3.2! = 6 , pois foi truncado em 2!, e como 2!=2.1 então temos que 3.2!=6.
Este segundo método facilita quando temos valores muito grandes e conhecemos os valores dos fatoriais menores.
b)
4!=4.3.2!
4!=4.3!
10!=10.9.8.7.6!
15!=15.14.13.12.11.10!
Exemplos III:
Exemplos IV:
Exemplos V:
Exemplos VI:
Agora vamos trabalhar com letras.
Primeiro vamos verificar qual dos fatoriais é o maior. Como eu faço para descobrir isto?
Vamos dar valores a variável k.
Exemplo:
Se k=1 , temos que:
(k+1)!=(1+1)!=2!=2, e do mesmo modo.
Se k=1 , temos que:
(k-1)!=(1-1)!=0!=1, (pela definição). Logo como 2 >1, então o maior fatorial é (k+1)!.
Como a definição de fatorial nos diz que o desenvolvimento de um fatorial vai de n até 1, significa que temos que desenvolver o fatorial de k+1 até atingir o fator (k-1)!.
Ou seja, vamos truncar k+1 em k-1, para poder simplificar nosso problema.
Definição - n!=n(n-1)!
Logo (k+1)!= (k+1).k!
Colocamos k+1 no lugar do n da definição.
Colocamos (k+1) no lugar de (n-1)! Da definição.
(k+1-1)!=k
Mas ainda não chegamos ao fator (k-1)! Para truncar.
Bem! Qual o fatorial de k, ou k!?
Voltamos mais uma vez a definição.
n!=n(n-1)! Logo colocando k no lugar de n, ou seja fazendo k=n na definição, temos.
K!=k(k-1)!. Viva!!!Acho que deu.
Vamos montar nosso problema agora.
Outros conteúdos sobre análise combinatória:
|
13/02/10
|
|
|
05/01/10
|
|
|
16/11/09
|
|
|
24/10/09
|
|
|
11/10/09
|
|
|
30/09/09
|
|
|
11/09/09
|
|
|
24/08/09
|
|
|
18/08/09
|
|
|
18/08/09
|
|
|
16/07/09
|
|
|
16/07/09
|
|
|
16/07/09
|
|
|
16/07/09
|
|
|
15/07/09
|
|
|
15/07/09
|
|
REFERÊNCIAS:
Tizziotti, José Guilherme, 1944, Matemática: Segundo grau, Volume II, 4ª edição - SP : Á tica, 1980.
Santos, J. Plínio O. Introdução à análise combinatória / J. Plínio O. Santos - 3ª ediçãoo SP: Unicamp, 2002.
Por enquanto ficamos por aqui. Em breve mais atualizações, aguarde!
Se você quer cooperar com dicas, indicar algum blog legal de matemática, programas legais que conhece, artigos, trabalhos de escola. Fique a vontade. Mande um e-mail para
caco36@ibest.com.br ,ou comente aqui mesmo. Por enquanto ficamos por aqui! Agradeço antecipadamente, comentários, dicas, criticas e sugestões.
Observação:
- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.
- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .

 , n!= n(n-1)(n-2)...1
, n!= n(n-1)(n-2)...1


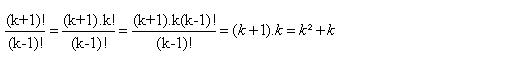
 Sobre a Autor:
Sobre a Autor:











Gostei do seu blog, pois trata de um assunto comum ao meu blog. Por isso, acho que devemos unir forças para divulgar as idéias matematicas, por isso, irei seguir o seu blog e ti convido a seguir o meu.
ResponderExcluirProf. Paulo Sérgio
www.fatosmatematicos.blogspot.com/ esse é o meu blog
ResponderExcluirOk Professor Paulo!Já passei no seu blog para dar uma espiada. Gostei bastante, pois acho que seguimos a mesma linha. No momento estou super, hiper ocupado, mas assim que estiver com mais tempo disponível, vou estar frequentemente blogando, e poderemos trocar idéias.
ResponderExcluirPesquisando na internet, encontrei o seu blog e gostaria de saber se está interessado em contribuir a um blog que estou montando com essas disciplinas: português, matemática, biologia, história, geografia, física, química e inglês.A divulgação das postagens se caso não queira divulgar fica por minha conta, há um espaço para os colaboradores divulgar seus sites pessoais. caso haja interesse comente em uma das postagens do blog: www.sofistablog.blogspot.com ou envie um e-mail para: blog_equipe@yahoo.com.br.
ResponderExcluirAdicionei seu blog na minha lista de blog. Parabens pela materia. Foi boa e se possivel, coloque um exemplo mostrando a necessidade de se usar o fatorial. Isto fecha com chave de ouro seu trabalho.
ResponderExcluirUm abraço
Domingos Lopes
softmatem.blogspot.com
Beleza Virgílio! A idéia é interessante, visto que se baseia no mesmo projeto em que estou trabalhando. No momento está só no papel, mas será implementado em breve.
ResponderExcluirO problema, é que estou com pouco tempo para amadurecer esta idéia, e não quero começar antes de ter todos os prós e contras no papel.
Já fiz parte de um grupo " O pensador selvagem" Onde tinha um blog com características semelhantes ao "matemática na veia", mas como já falei, o tempo era curto, e tive que abandonar o projeto.
Como deu para perceber,no momento não será possível juntar-se ao seu grupo de colaboradores. Mas fica a proposta, e se futuramente eu estiver em condições entrarei em contato com você.
Abraços.
http://matematica-na-veia.blogspot.com/
Obrigado pelo elogio professor Lopes! Com certeza! Ainda vou colocar mais alguns exemplos de exercícios com fatoriais. E vou dar um final com a sua idéia.
ResponderExcluirObrigado pela dica e participação aqui no "matemática na veia".
muito bom, nao conhecia seu brog, com certeza frequetarei mais vezes. parabens!!!
ResponderExcluirseria enteressante se voce colocasse tambem algumas coisas sobre geometria.
obrigado.
Josemar já estou escrevendo os artigos sobre geometria,mas será um novo Blog, O EGEOM. Em brave estará no ar. Abraços.
ResponderExcluirNossa muito bom..adorei tava com difilculdade agora estou mais a par da situacao ou seja a materia.
ResponderExcluir