Análise combinatória - Principio aditivo e multiplicativo

[♀]Matemática na Veia 2007-2016 O Blog do Estudante Inteligente

Relatos de erros e correções em relação ao português serão bem vindos e podem ser esclarecidos através do RH - Sugestões e Reclamações.

ANÁLISE COMBINATÓRIA

Introdução.

Em primeiro lugar vamos abordar estes dois principios que juntos do conceito de fatorial, que já foi visto anteriormente, são os alicerces da análise combinatória.

Principio aditivo e multiplicativo:

Vamos resolver alguns exercícios como exemplo, e gradualmente serão abordados alguns exemplos mais complexos.

Bom! Vamos começar com o principio aditivo.

PRINCÍPIO ADITIVO - DIVIDIR PARA SOMAR

Ex. 1 - Supondo que exista cinemas, e teatros em sua cidade, e que tenham entrado em cartaz 3 filmes e 2 peças de teatro diferentes para passarem no próximo sábado, e que você tenha dinheiro para assistir a apenas 1 evento destes 5 que foram descritos anteriormente. Quantos são os programas que você pode fazer neste sábado?

Vejamos então:

Vamos supor agora que cada programa custe apenas 1 real, e que você só tenha um real. Como você tem dinheiro para apenas um evento (programa), então ou você assiste ao filme 1 ou ao filme 2 ou ao filme 3 ou à peça de teatro 1 ou à peça de teatro 2.

A idéia é prestar atenção no conetivo “ou” do problema. Ou escolhe F1, ou escolhe F2, ou escolhe F3, e assim por diante.

Deste modo estamos dividindo o problema em casos. E como já citei anteriormente aparecerá a idéia do conetivo “ou”.

Caso eu escolher ver um filme, terei 3 opções ou caso eu escolher ver uma peça de teatro, terei 2 opções.

Como você pode observar os elementos de um conjunto não pertencem à outro, pois são distintos, logo eles são disjuntos. (A intersecção é vazia)

Logo pelo principio aditivo.

Se A e B são dois conjuntos disjuntos (A ∩ B = ø ) com respectivamente , f e t elementos, então A U B possui f+t elementos.

A={ f|f é um filme} = {F1,F2,F3}, e

B= { t|t é uma peça de teatro} = {T1,T2}

Logo A U B = { F1,F2,F3,T1,T2}

Assim ao todo são 3+2 = 5 programas.

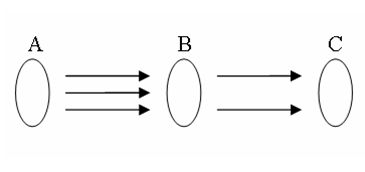
Vamos ver agora um exemplo com o principio multiplicativo.

PRINCÍPIO MULTIPLICATICO- DECISÕES EM SEQUÊNCIA

Ex. 2 – Supondo que você tenha agora dois reais, e quer assistir a um filme e uma peça de teatro, quantos são os programas que poderá fazer no sábado?

Bom! Repare que diferente do primeiro exemplo, neste você tem que tomar duas decisões em sequência.

1º decisão – escolher um filme dos três em cartaz.

2º decisão – escolher uma peça de teatro das duas disponíveis.

Vamos enumerar os casos possíveis:

Aqui a idéia é prestar atenção no conetivo “e”.

Filme 1 e Peça 1

Filme 1 e Peça 2

Filme 2 e Peça 1

Filme 2 e Peça 2

Filme 3 e Peça 1

Filme 3 e Peça 2

Logo você vai escolher um filme dos três em cartaz “e” escolher uma peça de teatro das duas disponíveis.

Logo pelo principio multiplicativo.

Se um evento A pode ocorrer de m maneiras diferentes e, se para cada uma dessas m maneiras possíveis de A ocorrer, um outro evento B pode ocorrer de n maneiras diferentes, então o nº de maneiras de ocorrer o evento A seguido do evento B é m.n

Logo você têm três vezes duas opções para escolher entre os programas.

Ou seja, 3.2=6 possibilidades.

Ex. 3 –  Vamos ver mais um exemplo com o Principio multiplicatico.

Vamos supor que você queira viajar este fim de semana, e que esteja pensando em ir para uma praia descansar. E no percurso até chegar a praia você tem que passar por uma outra cidade.

Vamos denotar a sua cidade por A, a cidade que você vai passar antes de chegar a praia por B, e a praia por C.

Supondo que existam 3 rotas diferentes até a cidade B e da cidade B até a praia existem 2 rotas diferentes.

De quantas maneiras possíveis você poderá chegar a praia usando um destes caminhos?

Acompanhe o exemplo abaixo.

De A para B temos 3 rotas, logo 3 possibilidades.Ou seja ao tomar a primeira decisão você têm 3 opções para escolher.

De B para C temos 2 rotas, logo 2 possibilidades. Ou seja após tomar a decisão A, você vai tomar uma 2º decisão B, onde você têm 2 possibilidades de escolha.

Logo pelo principio multiplicativo, temos 3 vezes 2 possibilidades. Ou seja você tem 6 possibilidades diferentes de ir até a praia passando pela cidade B.

Ex. 4 – Vamos misturar as coisas um pouco.

Vejamos um exemplo onde podemos trabalhar com os dois principios.

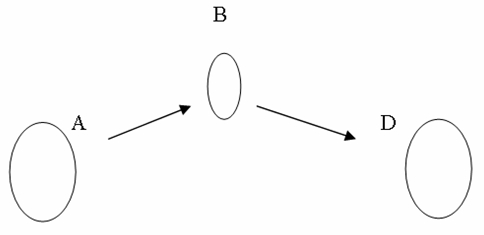
Supondo que você tenha que viajar, e tenha as seguintes opções observadas na figura abaixo. De quantas maneiras possíveis você poderá fazer a sua viagem escolhendo apenas um dos caminhos?

E agora José!!

Observe que temos casos diferentes.

1º - De A para D passando por B.

2º - Ir de A para D direto.

3º - De A para D passando por C.

Ué! Se temos casos diferentes vamos fazer por adição. Ou melhor vamos trabalhar com cada caso separadamente usando o Principio multiplicativo e logo após vamos somá-los.

1º - De A para D passando por B.

Tomamos a 1º decisão indo de A para B, na qual temos uma possibilidade( 1 caminho apenas)

Em seguida tomamos a 2º decisão indo de B para D, na qual temos também uma possibilidade (1 caminho apenas)

Logo temos 1.1 = 1 possibilidade de irmos de A até D passando por B.

2º - Ir de A para D direto.

Aqui ficou fácil! Temos apenas uma decisão para tomar e apenas duas possibilidades de escolha. Logo 1.2 =2 possibilidades de ir de A até D direto.

3º - De A para D passando por C.

Do mesmo modo, temos duas possibilidades de A para C e uma possibilidade de C para D. O que dá 2.1 possibilidades. Ou seja temos 2 Possibilidades Para ir de A até D passando por C.

Aplicando o Principio aditivo, temos 1+2+2 = 5 possibilidades. Ou seja 5 maneiras possíveis de viajar da cidade A até a cidade D.

Ir para Análise combinatória

Referências:

Tizziotti, José Guilherme, 1944, Matemática: Segundo grau, Volume II, 4ª edição - SP : Á tica, 1980.

Santos, J. Plínio O. Introdução à análise combinatória / J. Plínio O. Santos - 3ª ediçãoo SP: Unicamp, 2002.

* Com adaptações.

Por enquanto ficamos por aqui. Em breve mais atualizações, aguarde!

Se você quer cooperar com dicas, indicar algum blog legal de matemática, programas legais que conhece, artigos, trabalhos de escola. Fique a vontade. Mande um e-mail para caco36@ibest.com.br ,ou comente aqui mesmo. Por enquanto ficamos por aqui! Agradeço antecipadamente, comentários, dicas, criticas e sugestões.

Observação:

- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.

- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .

Share on Google Plus

Sobre a Autor:

Antonio Blogueiro desde 2007, gaúcho, gosta muito de ler, e é totalmente viciado em internet. Comecei blogar em 2005, e criei o Matemática na Veia no inicio de 2007. Sou formado em licenciatura Plena em Matemática pela UFPEL. Servidor Público,e fanático pela Web.