Phi - A razão aúrea e curiosidades matemáticas

[♀]Matemática na Veia 2007-2016 O Blog do Estudante Inteligente

Relatos de erros e correções em relação ao português serão bem vindos e podem ser esclarecidos através do RH - Sugestões e Reclamações.

PHI – A RAZÃO ÁUREA E ALGUMAS CURIOSIDADES

A Famosa Razão Áurea

 A razão áurea, ou " The golden ratio" em inglês, ou ainda "de divina proporcione", foi tema de investigação de inúmeros cientistas e curiosos, e um dos quais mais se destacou foi o famoso geômetra grego Euclides, autor de Os Elementos, primeira grande obra de geometria. Assim como o "PI” (Nosso grande amigo da trigonometria. O simbolo "π" ), o número "Phi" (razão áurea) é um número irracional. Este número tem sido motivo de estudo desde os mais remotos tempos. Ela representa, segundo os estudiosos, a mais agradável proporção entre dois segmentos ou duas medidas. Há muito essa proporção foi identificada, como sendo equivalente a 1,618: 1, e por convenção, é chamada de Phi.

Exemplo de lugares onde se encontra a razão áurea:

Filotaxia

A Proporção Divina também é encontrada em arranjos de folhas (Filotaxia).

Observamos a Golden Proportion nas folhas de uma planta. Elas são arranjadas de forma espiral ao longo do galho, não impedindo a luz do sol em nenhuma das folhas. A soma dos dois primeiros passos da espiral, começando do topo é igual ao tamanho do próximo passo, por exemplo, A+B=C, B+C=D, etc

(Fonte: L.Latishev e Vl. Latishev)

      FIGURA1                                                                                           FIGURA 2

Consideremos que exista um padrão helicoidal [para a esquerda ou para a direita] para as folhas em torno do caule. Cada conjunto de 3 folhas consecutivas [1,2,3] nascem formando um mesmo ângulo entre 1 e 2 e entre 2 e 3, mantendo uma certa distância ao longo do caule.

Na figura 2 , a folha 3 forma um mesmo ângulo com 2 da mesma forma que a folha 2 forma com 1. Admitimos o mesmo padrão para todas as folhas restantes.

Podemos identificar o período p como o número de voltas necessárias até nascer uma nova folha se sobrepondo à primeira e m indicará o número de folhas por período, neste caso, p=2 e m=5. Numerosas experiências com plantas mostraram que p e m assumem mais frequentemente valores como 1, 2, 3, 5, 8, 13, ..., que são os números da seqüência de Fibonacci.

Existem também exceções, mas os números de Fibonacci ocorrem tão freqüentemente que não podem ser explicados como casuais. Os biólogos tentaram explicar a predominância dos números de Fibonacci na Filotaxia. A simetria das folhas pode dar equilíbrio ao caule e também facilitar a exposição à luz, mas a ciência está longe de uma explicação satisfatória.

A Pirâmide de Quéops e a seção áurea.

As figuras abaixo mostram as proporções que os egípcios usavam nos cálculos da construção das pirâmides.

No inicio da construção da grande pirâmide, foi fixado sua orientação segundo a constelação da Mão de Touro [hoje Ursa Maior] estabelecendo uma linha em ângulo reto em relação a ela por meio de um retângulo 3:4:5, a partir dele, esboçavam todo o Templo.

A Seção áurea ou Pi, foi muito bem utilizada. Ela foi edificada com uma planta baixa quase perfeita de 775 pés e com ângulos de ascensão 51o 52'. Seu volume é de 6,5 milhões de toneladas de calcário. O ângulo de ascensão dá à Grande Pirâmide uma propriedade geométrica única, que representa a quadratura mística do círculo: sua altura está para a mesma razão da sua circunferência, assim como o raio para a circunferência de um círculo. Essa razão é ½ de Pi. Pi=3,1416, cujo número transcendental que está representado, assim está representado com uma margem de erro de apenas 0,1%.

Os Egípcios consideravam o número de ouro sagrado, tendo uma importância extrema na sua religião, e chamavam-no não de número de ouro, mas sim de "número sagrado". Utilizavam-no para a construção de templos e sepulcros para os mortos, pois consideravam que caso isto não acontecesse, o templo poderia não agradar os Deuses ou a alma do falecido não conseguiria chegar ao seu destino. Além disso, os Egípcios consideravam-no muito agradável esteticamente, usando-o também no seu sistema de escrita e na decoração dos seus templos.

O Papiro de Ahmes mostra-nos os planos para a construção da Grande Pirâmide de Gizé (4700 a.C.), com proporções de acordo com o "número sagrado". Medidas recentes desta pirâmide mostram que os lados da pirâmide parecem ser triângulos de ouro.

A Arte Egípcia

Durante a maior parte da história do Egito, as proporções da figura humana foram relacionadas com a largura da palma da mão, e baseavam-se no "número sagrado".

Os Egípcios usavam medidas estabelecidas pelas proporções do corpo humano devido ao fato de estas serem proporcionais, de acordo com a razão de ouro (0.618...), tornando as suas obras esteticamente mais agradáveis. Estas idéias foram utilizadas pelos construtores e artesãos, para estabelecer as malhas quadrangulares que usavam para as proporcionalidades do seu trabalho.

Os Hieróglifos

Muitos hieróglifos têm proporções baseadas no número de ouro. Os Egípcios utilizavam o número de ouro para que fosse mais fácil que todos conseguissem escrever de acordo com as mesmas proporções.

Na figura acima, a letra "h" é, de fato, uma espiral de ouro. Outros símbolos, como o "p" e "sh" são retângulos de ouro. O uso das mãos e dos pés nos hieróglifos mostra que os Egípcios tinham conhecimento que o corpo humano está relacionado de diversas formas com o número de ouro.

Algumas partes da anatomia humana onde podemos encontramos a proporção áurea.
Em destaque na imagem abaixo a mão humana e suas medidas proporcionais.

A altura do corpo humano e a medida do umbigo até o chão.
A altura do crânio e a medida da mandíbula até o alto da cabeça.
A medida da cintura até a cabeça e o tamanho do tórax.
A medida do ombro à ponta do dedo e a medida do cotovelo à ponta do dedo.
O tamanho dos dedos e a medida da dobra central até a ponta. A medida da dobra central até a ponta dividido e da segunda dobra até a ponta.
A medida do seu quadril ao chão e a medida do seu joelho até ao chão.

Essas proporções anatômicas foram bem representadas pelo "Homem Vitruviano", obra de Leonardo Da Vinci

O Homem Vitruviano é um desenho famoso que acompanhava as notas que Leonardo da Vinci fez ao redor do ano 1490 num dos seus diários. Descreve uma figura masculina desnuda separadamente e simultaneamente em duas posições sobrepostas com os braços inscritos num círculo e num quadrado. A cabeça é calculada como sendo um oitavo da altura total. Às vezes, o desenho e o texto são chamados de Cânone das Proporções.

O desenho atualmente faz parte da coleção/coleção da Gallerie dell'Accademia (Galeria da Academia) em Veneza, Itália.

O Homem Vitruviano é baseado numa famosa passagem do arquiteto/arquiteto romano Marcus Vitruvius Pollio na sua série de dez livros intitulados de De Architectura, um tratado de arquitetura em que, no terceiro livro, ele descreve as proporções do corpo humano:

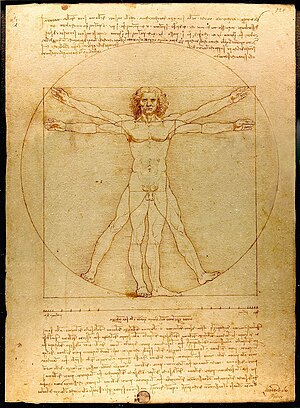
Fonte da imagem: Wikipédia

Construção geométrica sobre O Homem de Vitrúvio (1490); Leonardo da Vinci, pg.36.

Data: 1490 – Técnica: Lápis e tinta - Dimensão: 34 x 24 cm

"Os 4 dedos fazem uma palma e 4 palmas fazem 1 pé, 6 palmas fazem um cúbito; 4 cúbitos fazem a altura de um homem. 4 cúbitos fazem um passo e 24 palmas fazem um homem. Se abrir as pernas até termos descido 1/14 de altura e abrirmos os braços até os dedos estarem ao nível do topo da cabeça então o centro dos membros abertos será no umbigo. O espaço entre as pernas abertas será um triângulo eqüilátero. O comprimento dos braços abertos de um homem é igual à sua altura. Desde as raízes dos cabelos até ao fundo do queixo é um décimo da altura do homem; desde o fundo do queixo até ao topo da cabeça é um oitavo da altura do homem; desde o topo do peito até ao topo da cabeça é um sexto da altura do homem; desde o topo do peito até às raízes do cabelo é um sétimo da altura do homem; desde os mamilos até ao topo da cabeça é um quarto da altura do homem. A maior largura dos ombros contém em si própria a quarta parte do homem. Desde o cotovelo até à ponta dos dedos é um quinto da altura do homem e desde o cotovelo até ao ângulo da axila é um oitavo da altura do homem. A mão inteira será um décimo da altura do homem. O início dos órgãos genitais marca o centro do homem. O pé é um sétimo do homem. Da sola do pé até debaixo do joelho é um quarto da altura do homem. Desde debaixo do joelho até o início dos órgãos genitais é um quarto do homem. A distância entre o fundo do queixo e o nariz e entre as raízes dos cabelos e as sobrancelhas é a mesma e é, como a orelha, um terço da cara”. [texto que acompanha a gravura do Homem de Vitruvius]

A linha dos olhos que divide, nas pessoas bem conformadas, o comprimento total do rosto em média e extrema razão. Observa-se também a proporção divina nas partes em que as falanges dividem os dedos das mãos.

"Meçam a distância do ombro às pontas dos dedos, e então dividam-na pela distância do cotovelo às pontas dos dedos. Outra vez PHI. Mais uma? Anca ao chão a dividir por joelho ao chão. PHI. Articulação dos dedos das mãos. Dos pés. Divisões espinais. PHI, PHI, PHI. Meus amigos, cada um de vocês é um tributo ambulante à Proporção Divina." trecho retirado do livro "O Código Da Vinci".

Um dos quadros mais célebres de Leonardo da Vinci: Mona Lisa, pintado em, aproximadamente 1505, feito em madeira, 77 x 53 cm., Paris, Louvre. Também contém o número de Ouro, ou melhor, o retângulo de Ouro.

Definição Algébrica

A razão áurea é definida algebricamente como a+b/a=a/b=φ

A equação da direita mostra que, a=b φ o que pode ser substituído na parte esquerda. Temos, assim φb+b/bφ= bφ/b

Cancelando b em ambos os lados, temos. φ+1/ φ= φ

Multiplicando ambos os lados por φ nos dá φ+1= φ ²

Finalmente, arrumando os termos da equação, encontramos φ² - φ -1=0 que é uma equação quadrática da forma, a x ²+ bx+c = 0

Em que. a=1,b=-1 e c=-1

Agora, basta resolver esta equação quadrática. Pela Fórmula de Bháskara

A única solução positiva desta equação quadrática é , que é o número φ .

SEÇÃO ÁUREA :

Euclides de Alexandria descreveu esta seção em sua proposição "dividir um segmento de reta em média e extrema razão". Diz-se que o ponto B divide o segmento AC em média e extrema razão, se a razão entre o menor e o maior dos segmentos é igual à razão entre o maior e o segmento todo, isto é, AB/BC = BC/AC. Usando a notação moderna, podemos escrever esta relação assim:

Logo temos (a-x) / x = x / a

SEGMENTO ÁUREO:

Também chamado de segmento de ouro e número de ouro. É o segmento resultante da divisão de um outro segmento AB em média e extrema razão, ou seja, é obtido quando se faz uma seção áurea no segmento AB.

1. Quando se quer obter o segmento áureo (a) de outro segmento dado AB basta multiplicar (AB) por 1/f.

2. Quando se quer obter o segmento AB, onde (a) é o segmento áureo, é só multiplicar AB por f (f = número de ouro).

NÚMERO DE OURO:

Também chamado de razão áurea, seção áurea e segmento áureo; é simbolizado pela letra (f), inicial de Fídias, escultor grego que utilizou este número ou (t), tau. É o número obtido quando se divide (a) por (b)

(a+b) / a = a / b = f = 1,618034

F ² = 2,618

1 / f = 0,618034

Esta proporção diz que a relação entre a soma de duas grandezas, e uma delas (a maior, que no caso é "a"), é igual à relação entre esta (a) e a outra (b). Isto de fato se obtém quando a = 1,618, que é o número de ouro. Portanto 1,618 é a razão entre os termos da proporção.

É o único número positivo que satisfaz a relação f ² =1 + f.

A igualdade f = 2.cos.(p) implica a presença do número de ouro em muitas proporções.

EXEMPLOS:

Entre os elementos de polígonos regulares como: pentágonos, decágonos, estrelas pentagonais e decágonos. O número f aparece nas artes [retrato de "Isabelle d'Éste" pintado por Leonardo da Vinci], no pentágono regular estrelado, no corpo humano, animais, nas flores, na formação das árvores, na disposição das folhas em certas plantas, nos frutos, na espiral logarítmica, na construção do decágono regular, na construção do pentágono regular, em vários poliedros regulares, na pirâmide de Queops, nas danças clássicas, nas grandes catedrais da Idade Média, na Arquitetura, no "modulor" de Le Corbusier, na poesia, na série de Fibonacci.

RETÂNGULO ÀUREO:

É o retângulo que tem os seus lados a e b na razão áurea a/b = f = 1,618034, portanto, o lado menor (b) é o segmento áureo do lado maior (a).

CONSTRUÇÃO DO RETÂNGULO ÁUREO A PARTIR DO SEU LADO MAIOR

CONSTRUÇÃO DO RETÂNGULO ÁUREO A PARTIR DO SEU LADO MENOR

A construção do retângulo áureo é simples. Basta seguir o esquema:

O retângulo AHCG é áureo.

PENTÁGONO:

Do latim - pentagonum, do grego - pénta (cinco) + gon, de gônia (ângulo): péntagonos; é um polígono que possui 5 vértices, 5 lados e 5 ângulos.

DECÁGONO:

 Do grego - dekágonos, déka (dez) + gonia (ângulo), do latim - decagonu; é o polígono de dez vértices, dez lados e dez ângulos. Um fato de conhecimento dos antigos geômetras era que a razão do raio do círculo de um decágono regular para um dos lados é a razão áurea.

PENTAGRAMA:

Do grego - pénta (cinco) + gramma (linha); o símbolo da saúde e a insígnia que identificava os pitagóricos; é um pentágono regular estrelado onde cada um dos cinco segmentos divide outros em média e extrema razão. O ponto de intersecção P de duas diagonais divide cada uma delas na proporção áurea. P divide AQ e AB internamente e QB externamente nessa proporção.

TRIÂNGULO ÁUREO:

É um triângulo isósceles ABC com ângulos da base de 72º e ângulo do ápice de 36º

O triângulo áureo é encontrado no "pentagrama místico".

A partir do triângulo áureo podemos desenhar uma espiral logarítmica.

FIBONACCI:

Leonardo de Pisa, também chamado de Leonardo Fibonacci por ser filho de Bonacci (filius Bonacci); nasceu cerca de 1175 d.C.. Seus primeiros anos foram vividos em uma comunidade cristã, mas ele recebeu sua instrução acadêmica entre os maometanos da Barbaria. Ali conheceu o sistema arábico (ou decimal) de numeração, bem como os ensinamentos de álgebra de Alkarismi. Com cerca de vinte e sete anos de idade, retornou à sua terra natal e lá publicou uma obra amplamente conhecida como "Liber Abaci" (o livro do ábaco), na qual demonstrava as grandes vantagens do sistema arábico de numeração sobre o romano.

Esta obra de Fibonacci foi considerada obra-modelo durante duzentos anos e o principal veículo de introdução do sistema hindu-arábico de notação nas camadas cultas da Europa Cristã. Em sua obra "Liber Abaci", Fibonacci apresenta um quebra cabeça matemático que deu origem à série de Fibonacci relacionada com a criação de coelhos. Esta série segue a regra segundo a qual cada termo é a soma dos dois termos imediatamente anteriores:

Un+1=Un+Un-1(U0= 0, U1=1)

Ex..: 1 : 1 : 2 : 3 : 5 : 8...

Um poema - O misterioso número de ouro

Do número nasce a proporção

                                                              Da proporção se segue à consonância 

               A consonância causa deleitação 

                                                                      A nenhum sentido apraz a dissonância 

     Unidade, igualdade e semelhança 

                                                          São princípios do contentamento

           Em todos os sentidos o experimento

                                                                       A alma na unidade glória alcança

        Em todas as quantidades a igualdade 

                                                   E a perfeição remota ou a mais chegada

Segundo a natural autoridade

                                                       E assim esta nas qualidades assentada

Da mesma maneira a semelhança

                                                                   Diva de ser sentida e contemplada

[Vasco Graça Moura, Camões e a Divina Proporção]

De quebra vou deichar dois Vídeos sobre o número de ouro para vocês se deleitarem.

Em breve mais atualizações, aguarde.

Assine aqui, o Feed do Matemática Na Veia , e receba por e-mail os artigos do blog. Fique por dentro das novidades, e curiosidades da matemática

Se você quer cooperar com dicas, programas, artigos. Fique a vontade, e mande um e-mail para caco36@ibest.com.br ,ou comente aqui mesmo, por enquanto ficamos por aqui, Agradeço antecipadamente, comentários, dicas, criticas e sugestões.

Observação:

- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.

- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .

Share on Google Plus

Sobre a Autor:

Antonio Blogueiro desde 2007, gaúcho, gosta muito de ler, e é totalmente viciado em internet. Comecei blogar em 2005, e criei o Matemática na Veia no inicio de 2007. Sou formado em licenciatura Plena em Matemática pela UFPEL. Servidor Público,e fanático pela Web.