COEFICIENTES BINOMIAIS
Nos artigos anteriores em análise combinatória, tratamos de Binômios de Newton e sobre, como trabalhar com a fórmula do Binômio de Newton, e noutro artigo, também vimos a biografia de Niccolo Tartaglia, um dos matemáticos mais promissores do século XVI, e também, responsável pelos primeiros estudos sobre o número de combinações possíveis para um determinado fenômeno. Deste artigo em diante vamos trabalhar com algumas propriedades dos números binomiais, ou como alguns autores preferem coeficientes binomiais. As propriedades sobre os números binomiais serão divididas em três textos (aulas), cada uma com desenvolvimentos da propriedade a que se refere o tema, além de exercícios com resoluções detalhadas e gabarito no final do texto.Começamos com o tema principal “número binomial”, e posteriormente veremos “binomial complementar” e “binomial consecutivo” respectivamente.
NÚmeros Binomiais :
Dados dois números naturais n e k , com n ≥ k , o número 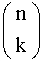 é chamado de número binomial, ou binomial n sobre k definido da seguinte forma:
é chamado de número binomial, ou binomial n sobre k definido da seguinte forma:
O número binomial também é chamado de coeficiente binomial.
O número n é o numerador do binomial e k é chamado classe do binomial. Observe os exemplos de alguns números binomiais.
Observações:
Como vimos Cn,0 é a quantidade de subconjuntos com 0 elementos que se pode obter de um conjunto de n elementos. Com 0 elementos só existe um subconjunto que é Ø
Exemplos:
E1-Exercícios:
1- Calcule:
 GABARITO:
GABARITO:
a) 56 b) 220 c) 190 d) 10 e) 1 f) 1 g) 1 h) n
Por enquanto ficamos por aqui. Em breve mais atualizações, aguarde!
Se você é aluno, professor, ou simplesmente um apaixonado pela matemática, e quer cooperar com dicas, indicar algum blog legal de matemática, ou que seja relacionado a educação, programas legais que conhece, artigos, trabalhos de escola. Fique a vontade. Mande um e-mail para
caco36@ibest.com.br ,ou comente aqui mesmo. Agradeço antecipadamente, comentários, dicas, criticas e sugestões.
Observação:
- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.
- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .
REFERÊNCIAS:
BACHX, A. de; POPPE, L. M. B.; TAVARES; RAYMUNDO N. O. – Prelúdio à Análise Combinatória. Companhia Editora Nacional. 1975
CARVALHO, P. C. P; LIMA, E. L.; MORGADO, A. C; WAGNER, E. – A Matemática do Ensino Médio. Vol. 2. Coleção do Professor de Matemática. Sociedade Brasileira de Matemática. 1998
CARVALHO, J. B. P; CARVALHO, P. C. P; FERNANDEZ, P; MORGADO, A. C de O. – Análise Combinatória e Probabilidade. Coleção do Professor de Matemática.
 Sobre a Autor:
Sobre a Autor:
Antonio
Blogueiro desde 2007, gaúcho, gosta muito de ler, e é totalmente viciado em internet.
Comecei blogar em 2005, e criei o Matemática na Veia no inicio de 2007.
Sou formado em licenciatura Plena em Matemática pela UFPEL. Servidor Público,e fanático pela Web.
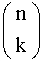 é chamado de número binomial, ou binomial n sobre k definido da seguinte forma:
é chamado de número binomial, ou binomial n sobre k definido da seguinte forma:



 Sobre a Autor:
Sobre a Autor:











Olá!
ResponderExcluirAcompanho esse blog a algum tempo e posso dizer que você fez um excelente trabalho. Hoje lí um artigo do site Inovação Tecnológica e me lembrei do Matemática na Veia. Veja:
http://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=cientistas-resolvem-problema-alem-capacidade-computadores&id=010150090923
Valeu Victor! Li o artigo um pouco atrasado, mas gostei bastante, pois acredito que um dia as máquinas superarão o homem. Espero que demore bastante!
ResponderExcluirAbraços.
Respondar essas questões pra min
ResponderExcluir