Biografia de Nicolo Fontana de Brescia - Tartaglia

[♀]Matemática na Veia 2007-2016 O Blog do Estudante Inteligente

Relatos de erros e correções em relação ao português serão bem vindos e podem ser esclarecidos através do RH - Sugestões e Reclamações.

Nicolo Fontana de Brescia - Tartaglia

Niccolò Tartaglia [ nēk-kōlô' tärtä'lyä , pseudônimo de Niccolò Fontana, (Brescia, c. 1499 — Veneza, 13 de dezembro de 1557) foi um matemático italiano, cujo nome está ligado a tabela triangular mais conhecida como “Triângulo de Pascal”.

Nicolo Fontana de Brescia, mais conhecido por Tartaglia, nasceu em Brescia por volta de 1500 e morreu em Veneza em 1557. Seu pai, Michele Fontana, morreu em 1506 quando Tartaglia tinha apenas 6 anos, deixando sua viúva, dois filhos e duas filhas na pobreza. O seu apelido Tartaglia, tem uma história curiosa, que ele mesmo conta no seu livro “Quesiti et inventioni diverse” e que, em resumo, é a seguinte: Em 1512, quando os franceses invadiram Brescia durante a Guerra da Liga de Cambrai. Comandadas por Gaston de Foix. A milícia de Brescia conseguiu defender a sua cidade por sete dias. Até o final desta sangrenta batalha, mais de 45.000 moradores da cidade de Brescia foram mortos. Durante o massacre, Nicolo procurou refugio, com a mãe e a irmã, na igreja da cidade, julgando ser um sítio seguro. Mas os soldados nem esses locais pouparam e Nicolo, diante da própria mãe, foi gravemente ferido com golpes de sabre e abandonado moribundo entre os cadáveres. O menino sofreu ferimentos na cabeça e na face, o que ocasionou em um profundo corte na mandíbula e palato.

A mãe, viúva e sem meios para pagar a um médico, tratou-lhe das feridas, com a sua própria saliva, do mesmo modo que os animais tratam os seus filhotes. Nicolo salvou-se, mas devido às sequelas do grave ferimento, ficou definitivamente com grande dificuldade na fala, tendo assim ficado com a alcunha de Tartaglia, que significa “tartamudo”, ou em bom português, simplesmente “gago”. Esse nome ficou-lhe durante muito tempo como lembrança da sua desgraça e, por isso, resolveu adotá-lo, passando a chamar-se Nicolo Tartaglia. Como podemos observar, ele usava uma longa barba, a qual usava para esconder suas terríveis cicatrizes. O próprio Tartaglia cita em um dos seus livros a seguinte frase, “Se minha barba não escondesse minhas cicatrizes, eu pareceria um monstro”.

Oriundo de uma família muito humilde, e com poucos recursos financeiros, tornou-se autodidata, onde só aos catorze anos e pelos próprios meios aprendeu a escrever, mas isso não foi obstáculo para que viesse a ser, engenheiro agrimensor, guarda-livros e a ensinar matemática em cidades italianas como Verona, Veneza, Piacenza e Brescia, – Foi professor de Galileu galilei em Florença- .Além disso, criou importantes trabalhos, onde demonstrou muito dos conhecimentos adquiridos nas áreas de aritmética, geometria, álgebra, balística e estática.

Sendo possivelmente, o único professor de matemática em Veneza, Tartaglia aos poucos foi adquirindo uma reputação promissora como matemático, devido às suas bem sucedidas participações em inúmeros debates públicos e concursos matemáticos onde ganhou diversos prêmios.

Foi pioneiro na aplicação da matemática à artilharia bélica, e em 1537, foi impressa a sua primeira obra “Nova scientia inventa” que se refere à balística, no qual considerou que os movimentos, natural e violento, aristotélicos eram compatíveis; desse modo, utilizou-os para explicar o movimento oblíquo de projéteis cuja trajetória seria, então, composta de uma parte retilínea (correspondente à parte violenta), seguida de uma parte circular (mista) e, por fim, de uma parte vertical (correspondente ao aspecto natural do movimento). Para Tartaglia, o efeito mais longínquo, ou seja, o alcance máximo é medido entre o ponto de partida e o ponto onde começa a vertical e que, tal distância, pode corresponder a duas inclinações diferentes do canhão lançador do projétil, sendo mínima para 90° e máxima para 45°.

Antes de Tartaglia, Leonardo da Vinci havia estudado a ciência da balística, mas seu trabalho não era tão abrangente. Em sua análise da dinâmica dos corpos em movimento, Tartaglia diferenciou vários tipos de movimentos distintos.

Desenhos criados por Tartaglia sobre o estudo de peças de artilharia. Este estudo dizia respeito às várias formas das peças e dos diferentes materiais usados em projéteis de artilharia usados na época. O livro foi escrito em italiano por Tartaglia, e traduzido para o idioma inglês por Cipriota Lvcar. 

Balança tipo “Stater” usada na época. (Trapézio).

Como havia vários tipos e tamanhos de materiais envolvidos nos estudos de Tartaglia foi necessário construir uma balança para pesar as peças de artilharia – Neste caso canhões-.

A Tartaglia também é atribuído o desenvolvimento do primeiro método geral para resolver equações cúbicas (equações do terceiro grau). Ele escreveu o tratado sobre balística – citado anteriormente- para determinar que o intervalo máximo de uma peça de artilharia D corresponde a um ângulo de disparo de 45 °, foi autor também de um tratado geral de números e medidas (1543) publicando pela primeira vez o triângulo que leva seu nome (também conhecido como triângulo de Pascal).

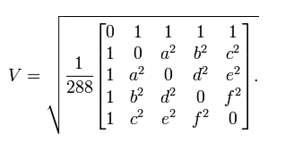
 (trabalho posteriormente confirmado pelos estudos realizados por Galileu), bem como pela expressão matemática para o cálculo do volume de um tetraedro, em termos do comprimento de seus lados, conhecida como fórmula de Tartaglia, uma generalização da fórmula de Heron (usado para calcular a área do triângulo): (incl. Quaisquer tetraedros irregulares) como o determinante de Cayley-Menger.

  A fórmula de Heron. 

   

  A fórmula de Tartaglia.Onde d_ij é a distância entre os vértices i e j.

 

Seguiu-se em 1546, o “Quesiti et inventioni diverse “ , que tem a forma dialogada e inúmeras notas autobiográficas de caráter geral, no qual modificou algumas explicações tratadas sobre o movimento oblíquo de projéteis, passando a defender uma trajetória totalmente curvilínea, que já havia sido considerada por Leonardo da Vinci. Para explicar essa trajetória, Tartaglia admitiu a hipótese de que quanto mais rapidamente o projétil se desloca, mais pesado se torna e, portanto, mais fortemente é puxado pela Terra. Ainda nesse livro, Tartaglia deu continuidade aos estudos de corpos em queda livre e em planos inclinados, iniciados na obra  “Nova scientia inventa” de 1537.  Nesses estudos afirmou que, “Todos os corpos graves semelhantes e iguais partem do início de seu movimento natural com a velocidade igual, mas aumentam suas velocidades de maneira tal que, aquele que atravessar um espaço maior, se deslocará mais rapidamente". Afirmou também que, “Quanto mais um corpo grave se afasta do princípio ou se aproxima do fim do movimento violento, mais lentamente ele se desloca". Ao analisar o movimento de um corpo através de um hipotético buraco feito na Terra e passando pelo seu centro, concluiu que “tal corpo ficaria oscilando em torno do centro de nosso planeta, diminuindo gradualmente sua velocidade, até parar". Com relação ao movimento de um corpo em um plano inclinado, observou que a gravidade natural do corpo colocado em tal plano age tanto menos, quanto maior for sua inclinação. É também de Tartaglia a afirmação de que um corpo em movimento circular, uma vez solto, tomará a direção da tangente, considerando questões que lhe tinham sido colocadas. A obra, na sua maior parte, tratava de questões de engenharia e arte militar, mas abundavam também questões matemáticas.

“Quesiti et inventioni divers”

 

 

Detalhes sobre o livro. Em italiano:

http://it.wikisource.org/wiki/Quesiti_et_inventioni_diverse

Uma dessas questões conduzia a uma equação do 4ºgrau, precisamente aquela que viria a ser mais tarde resolvida por Ferrari. Histórica e tecnicamente importantes são as suas referências à resolução da equação cúbica. Por último figuram no “ Quesiti et inventioni divers” a sua disputa com Fior, algumas das questões que faziam parte dessa disputa, e o seu encontro com Cardano no qual Tartaglia supostamente lhe  entregou os “Tercetos “ com a solução da cúbica de sua autoria.

Do ponto de vista técnico deduz-se que para além dos resultados conseguidos com as regras que se encontravam, nos “Tercetos” deve-se a Tartaglia a redução de qualquer equação cúbica trigonométrica a uma das três a que se aplicavam as suas regras.

No entanto não havia referência nenhuma nos seus escritos ao caso irredutível, nem tão pouco ao caso geral da equação cúbica completa.

São tais questões que Tartaglia trata na sua obra “ la travagliota inventione” de 1551, assim como também os deveria ter tratado na sua obra máxima, o “ Tratado general de números y de medidas”, que foi publicado em 1556 , o qual é considerado o melhor trabalho sobre a aritmética escrita na Itália, em seu século. Dos seis volumes aparecidos, os últimos quatro são postulados e o último deles não foi relatado por Tartaglia, mas sim por um outro “doutor matemático” tendo por base os apontamentos de Tartaglia. Este tratado é uma obra enciclopédica do tipo da “Summa” de Pacioli. Os dois primeiros volumes referem-se à aritmética teórica e prática. A última parte do tratado refere-se à álgebra, mas infelizmente termina com as equações quadráticas sem entrar nas cúbicas.

Elaborou o "Tratado Geral dos Números e  Medidas" – já citado anteriormente- (1556-1560), que contém regras de aritmética, álgebra, geometria e física. Publicou “Travagliata inventione” (1551).

Para além destas obras e dos “Contracartelli” aparecidos devido à polêmica com Ferrari, deve-se a Tartaglia a primeira edição italiana dos “Elementos de Euclides” - uma anterior de Pacioli ter-se-ia perdido, assim como versões e edições de obras de Arquimedes e de Jordanus Nemorarius.

Síntese dos trabalhos publicados por Tartaglia:

"Scienza Nuova", lidando com artilharia (Veneza, 1537, tradução francesa por Rieffel, Paris, 1845-6), a primeira tradução para o italiano de obras de Euclides (Veneza, 1543), 
tradução da primeira versão latina de algumas das obras de Arquimedes (Veneza, 1543); 
"Quesiti ed Invenzioni Diverso", incluindo problemas de balística e de fortificação (Veneza, 1546, nova ed., 554);  
"Regola Generale per ogni sollevare affondata Nave, intitolata la Travagliata Invenzione" (Veneza, 1551, versão em Inglês publicado pela Salusbury, Londres, 1564); 
"Ragionamenti sopra la Travagliata Invenzione" (Veneza, 1551);  
"Trattato Generale di Numeri e Misure" (Veneza, 2 pts. em 1556, 4 pts. em 1560);  
"Trattato di aritmetica" (Veneza, 1556, tr francês. por Gosselin, Paris, 1578);  
"Opere del Famosissimo Nicolò Tartaglia" (Veneza, 1606), e uma tradução para o Inglês, por Lucar em 1588, de seus escritos balísticos. 
Uma carta de Tartaglia está nos arquivos de Urbino e outra carta e seu testamento estão nos arquivos de Veneza.

Observação a respeito da pronúncia do nome de Tartaglia:

 Tartaglia : Lê-se [ta'talya].

Algumas curiosidades a cerca da notação usada por Tartaglia.

Tartaglia usava os seguintes símbolos:

- Ao invés de escrever + escrevia p;

- Ao invés de - escrevia m;

Na época de Tartaglia, as letras p (piu) e m (meno) eram usadas na Itália para indicar a adição e a subtração.

- Para a incógnita usava a letra R;

- Ao invés do sinal = escrevia equale - ou seja, igual em latim-;

- Quando escrevia um número isolado, acrescentava a letra N para significar a unidade.

Por enquanto ficamos por aqui. Em breve mais atualizações, aguarde!
Se você é aluno, professor, ou simplesmente um apaixonado pela matemática, e quer cooperar com dicas, indicar algum blog legal de matemática, ou que seja relacionado a educação, programas legais que conhece, artigos, trabalhos de escola. Fique a vontade. Mande um e-mail para caco36@ibest.com.br ,ou comente aqui mesmo. Por enquanto ficamos por aqui! Agradeço antecipadamente, comentários, dicas, criticas e sugestões.

Observação:

- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.

- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .

REFERÊNCIAS:

http://www.matematica-na-veia.blogspot.com/2008/01/crolnologia-da-histria-da-matemtica.html
http://www.educ.fc.ul.pt/docentes/opombo/seminario/renascenca/tartaglia.htm
http://perso.wanadoo.es/frs88/
http://es.wikipedia.org/wiki/Niccol%C3%B2_Fontana_Tartaglia
http://www.answers.com/topic/niccolo-fontana-tartaglia
http://archimedes2.mpiwg-berlin.mpg.de/
http://en.wikisource.org/wiki/Main_Page
http://www.answers.com/topic/binomial-coefficient
http://www.cbi.umn.edu/
http://www.sbfisica.org.br/
http://www.history.navy.mil/library/special/pre1700.htm

Share on Google Plus

Sobre a Autor:

Antonio Blogueiro desde 2007, gaúcho, gosta muito de ler, e é totalmente viciado em internet. Comecei blogar em 2005, e criei o Matemática na Veia no inicio de 2007. Sou formado em licenciatura Plena em Matemática pela UFPEL. Servidor Público,e fanático pela Web.