Potenciação com expoentes racionais,irracionais e reais

[♀]Matemática na Veia 2007-2016 O Blog do Estudante Inteligente

Relatos de erros e correções em relação ao português serão bem vindos e podem ser esclarecidos através do RH - Sugestões e Reclamações.

POTÊNCIA COM EXPOENTE RACIONAL

No artigo de hoje veremos qual o significado da representação de potência racional onde a^q , com a positivo e p = m/n é um número racional, m ∈ Z , n ∈ Z^* , de modo que a propriedade fundamental vista nos tópicos anteriores continue válida.

O conjunto dos números racionais é formado por todos os números que podem ser escritos na forma  m/n , onde m é um número inteiro qualquer e n um número inteiro qualquer diferente de zero.  É indicado pela letra maiúscula Q, e representado da seguinte forma:

Q = {x | x = m/n, m ∈ Z , n ∈Z^*} 

De modo geral, baseando-se na propriedade fundamental, temos:  a^p .a^q = a^p+q , deste modo, fazendo p = 1/n , teremos :

Vejamos alguns exemplos:

Do mesmo modo anterior, preservando a propriedade fundamental, e fazendo p = m/n, teremos:

Vejamos exemplos da definição acima:

Potência com expoente irracional

Trabalhamos até agora com expoentes naturais, inteiros e racionais vistos no início deste artigo. Veremos agora uma forma de caracterizar potências com expoentes irracionais, ou seja, números que pertencem ao conjunto dos números irracionais.

Veja alguns exemplos de números irracionais:


Usando a relação de Pitágoras, podemos representar alguns destes valores sobre a reta numérica.

Quando o teorema de Pitágoras é aplicado a um triângulo com dois lados que equivalem a um, tem-se como resultado a hipotenusa dada peça equação c² = 1²+1² = 2 , logo temos que c =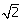  

Representação geométrica da raiz quadrada de 2

Curiosidades 1 :

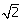
Acredita-se que tenha sido o primeiro número irracional reconhecido como tal. Esta importante descoberta é atribuída a Hipaso de Metaponto, da escola de Pitágoras. Conta-se mesmo que a demonstração tenha custado a vida de seu descobridor, uma vez que contrariava as idéias predominantes entre os pitagóricos de que tudo era número inteiro.

Fonte:http://pt.wikipedia.org/wiki/Raiz_quadrada_de_dois 

Fica evidente que nem sempre a raiz de um número racional é um número racional.  Para que a teoria dos números racionais evoluísse foi necessário o avanço dos estudos sobre infinitos e geometria analítica. Foram alguns séculos para que, entre tantas contribuições, chegássemos ao século xix com Dedekind (J.W.R. Dedekind, 1831-1916) e Cantor (George Cantor, 1845-1918), dando rigor científico a esta teoria.

            Curiosidades 2 :

- O número p (PI) é obtido dividindo-se a medida do comprimento de qualquer circunferência pela medida de seu diâmetro.

- O número irracional p (PI) foi calculado com o auxílio de um computador, obtendo-se 1,2 trilhões de casas decimais sem que tenha surgido uma decimal exata ou dizima.  

Para facilitar os cálculos podemos usar uma calculadora, e verificar que:

2¹        =  2

2^1.4     = 2,639015,

2^1.41   = 2,657371,

2¹⁴¹⁴  = 2,664749, ...       = 2,665144...
 

Desta forma obtemos por aproximação de racionais, a potência de aⁿ , com n irracional e a um número real positivo. 

História DOS IRRACIONAIS:

“Filolau, filósofo pitagórico (século IV a.C.) , foi um dos primeiros a escrever sobre os números irracionais. Segundo ele, e outros eruditos que viveram em épocas posteriores aos pitagóricos, os números irracionais foram descobertos por Pitágoras e seus discípulos. A existência de tais números foi deduzida do famoso TRIÂNGULO DE PITÁGORAS. Os pitagóricos perceberam que era impossível escrever o número obtido como razão de dois números inteiros. Na época em que a avassaladora descoberta foi feita, os pitagóricos constituíam uma sociedade bem estabelecida, dedicada ao estudo do poder e do mistério dos números...”

Fonte:  ACZEL, Amir D. O mistério do Alef : A matemática, a cabala e a procura pelo infinito. Editora Globo S.A. , 2003. Titulo original: The mistery of the Aleph

POTÊNCIA COM EXPOENTE REAL.

Até o momento vimos como trabalhar com potências nos conjuntos numéricos dos números naturais, inteiros, racionais e irracionais. Agora veremos um pouco sobre os números reais revendo algumas propriedades através de alguns exercícios. Os números racionais unidos com os irracionais resultam no conjunto dos números reais, pois todo número racional ou irracional é também um número real.

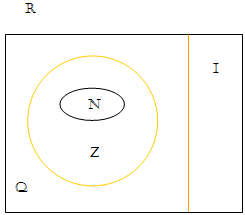
Veja a figura abaixo, onde temos a união dos conjuntos racionais representados pela letra maiúscula Q e os irracionais representados pela letra maiúscula I.

Observe que através da representação do conjunto universo, podemos interpretar  as propriedades vistas nos conteúdos anteriores, que  devem ser mantidas quando trabalhamos no conjunto dos reais. São exemplos de potências com expoentes reais:

Observação: Quando a=0 ou a < 0, algumas potências de base a estão definidas em R, mas outras não. Por exemplo:

Como os números reais são o resultado da união dos números racionais e dos números irracionais, a potência com expoente real será o resultado das definições vistas para estes conjuntos respectivamente. 

Vamos praticar um pouco revisando através de exercícios!    Para conferir seus resultados use as calculadoras do blog.        

Veja os exercícios nos arquivos para downloads. 

IR PARA O CONTEÚDO  POTENCIAÇÃO

Tópicos do conteúdo:

1 - Potenciação:Histórias e Rimas 
2 - Potência de expoente natural: Introdução.
3 - Potência de expoente inteiro. 
4 - Potências de números Racionais,Irracionais e Reais. 

DOWNLOAD: Espere 60 segundos e clique em baixar.

Exercícios básicos de potências de números Naturais com gabaritos  

Exercícios básicos de potências de números Inteiros com gabaritos Conteúdo deste artigo em formato PDF (Acrobat Reader)

Exercícios de revisão com gabarito : Download
 

Por enquanto ficaremos por aqui. No próximo artigo vamos descobrir algumas aplicações que envolvem as propriedades do triângulo Aritmético.  

Se você é aluno, professor, ou simplesmente um apaixonado pela matemática, e gostaria de cooperar com dicas, indicar algum blog legal de matemática, ou que seja relacionado à educação, programas legais que conhece, artigos, trabalhos de escola. Mande um e-mail para caco36@ibest.com.br,ou comente aqui mesmo. Agradeço sua cooperação, comentários, dicas, críticas e  sugestões.

Este artigo está em constante atualização, portanto assine o FEED do blog para receber as atualizações gratuitamente. 

BIBLIOGRAFIA:

GIOVANNI, José Ruy; CASTRUCCI, Ângela (org). Por trás da porta, que a matemática acontece. Campinas:UNICAMP , 2001.

IMENES, Luiz. ; LELLIS, Marcelo. Matemática. 5^a a 8^a  série . Scipione, 1998.

BIGODE, Antonio José Lopes, 1955 – Matemática hoje é feita assim / Antonio José Lopes Bigode, - São Paulo:FTD, 2000. 5^a série.

GIOVANNI, José Ruy; 1937 – A conquista da matemática – Nova / José Giovanni, Benedito Castrucci, José Ruy Giovanni Jr. – São Paulo: FTD, 1998.

IMENES, Luiz. ; LELLIS, Marcelo. Matemática. 5^a a 8^a  série . Scipione, 1998. 

Share on Google Plus

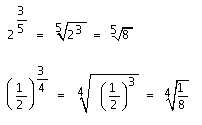
Sobre a Autor:

Antonio Blogueiro desde 2007, gaúcho, gosta muito de ler, e é totalmente viciado em internet. Comecei blogar em 2005, e criei o Matemática na Veia no inicio de 2007. Sou formado em licenciatura Plena em Matemática pela UFPEL. Servidor Público,e fanático pela Web.