Potenciação : Um pouco de história e rimas

[♀]Matemática na Veia 2007-2016 O Blog do Estudante Inteligente

Relatos de erros e correções em relação ao português serão bem vindos e podem ser esclarecidos através do RH - Sugestões e Reclamações.

Potências

  

         Um pouco de história

         “... A utilização da palavra ‘potência’, no contexto da matemática, é atribuída a Hipócrates de Quio (470 a.C.), autor que escreveu o primeiro livro de geometria elementar do qual, provavelmente, os Elementos de Euclides recolheram uma importante inspiração. Hipócrates designou o quadrado de um segmento pela palavra dynamis, que significa precisamente potência. Existem motivos para se crer que a generalização do uso da palavra potência resulte do fato dos Pitagóricos terem enunciado o resultado da proposição I.47 dos Elementos de Euclides sob a forma: “a potência total dos lados de um triângulo retângulo é a mesma que a da hipotenusa”.

         Portanto, o significado original de “potência” era potência de expoente dois, somente passadas algumas décadas se conceberam potências de expoente superior (Ball, 1960). Arquimedes (250 a.C.) no seu livro Contador de areia pretendia determinar o número de grãos de areia necessários para encher o universo solar, o que para ele consistia numa esfera tendo a Terra como centro e a sua distância ao Sol como raio. Obteve a solução 10⁵¹ que não podia ser escrita na numeração utilizada na altura (alfabética), uma vez que apenas permitia escrever números até 10.000 (uma miríade).

         Arquimedes criou então um novo sistema: considerou os números de 1 a 10 ⁸ , ou seja, até uma miríade de miríade, que se podiam escrever na numeração grega como sendo de primeira ordem; depois, os números de 10⁸ até 10 ¹⁶  como sendo de segunda ordem, em que a unidade é 10⁸, e assim, sucessivamente (Boyer, 1989). Arquimedes utilizou deste modo, uma regra equivalente à propriedade da multiplicação de potências com a mesma base: 10⁵¹ =10³ .10⁸ .10⁸ .10⁸ .10⁸ .10⁸ .10⁸ .... ”.

       “...Uma das primeiras referências à operação de potenciação encontra-se num papiro egípcio que remonta ao final do Império Médio (cerca de 2100 a 1580 a.C.). Ao ser ali apresentado o cálculo do volume de uma pirâmide quadrangular, é usado um par de pernas como símbolo para o quadrado de um número (Ball, 1960). A noção de potência era, também, conhecida dos babilônios. Recordando o seu sistema de numeração sexagesimal, observe-se o conteúdo de uma antiga tabuinha babilônica de argila conhecida como a tabuinha de Larsa e a respectiva tradução (Fauvel, 1987, p. 22):

       Figura  - Placa de Larsa  (Extraído de Fauvel, 1987). 

          Em outras tábuas antigas encontraram-se tabelas contendo as potências sucessivas de um dado número. Estas eram utilizadas para resolver certos problemas de astronomia e de operações comerciais, tais como: Quanto tempo levará a duplicar certa quantia de dinheiro, a uma taxa anual de 20 %? ...  ”

Fonte: Oliveira, H., & Ponte, J. P. (1999). Marcos históricos no desenvolvimento do conceito de potência. Educação & Matemática, 52, 29-34.

 AS OPERAÇÕES BÁSICAS.

Sabemos que as operações básicas da aritmética são: adição, subtração, divisão e multiplicação. Através do processo de multiplicação podemos encontrar outras operações: Uma delas é a potenciação. Potenciação é sinônimo de multiplicação repetida. Preste atenção nos exemplos abaixo:

Veremos no decorrer do conteúdo abordado todas as propriedades relacionadas à potenciação, bem como algumas curiosidades e macetes, como o apresentado no exemplo anterior. Também veremos diversos exercícios com desenvolvimentos detalhados, e muitos outros problemas resolvidos com seus respectivos gabaritos disponibilizados para download. Tudo isso para ajudá-lo a se preparar melhor para suas provas de matemática.

POTÊNCIA RIMADA 

Antes de tratarmos do conteúdo de potências, e suas propriedades propriamente ditas, vamos dar uma voltinha pela história da matemática e descobrir alguns aspectos interessantes que podem ser de bastante utilidade para o nosso aprendizado.É claro! Que se você é um dos poucos que não se interessam pelas histórias, curiosidades e belezas da matemática; fique a vontade para ir direto para as definições, propriedades, e exercícios relacionados ao tema “Potências”. Mas posso lhe garantir que você estará perdendo a essência das grandes descobertas, realizadas pelos milhares de pensadores e pesquisadores nos últimos 4.000 anos de história da humanidade.

Vamos ao que interessa então!  Vejamos o seguinte verso:
Vamos fazer uma perguntinha básica para você em forma de rima. Tente responder antes do sinal tocar. Relaxe um pouco antes de responder a pergunta.

Humor e Pizza em Brasília.

Imagem: Pizzaiolos tupiniquins preparando pizzas para os brasileiros

          Fonte: http://www.mistertube.com.br/

A voz do Brasil, o seu jornal radiofônico, em seu horário nobre, apresenta mais uma parte do épico “Em Brasília são dezenove horas”. Uma pergunta respondida vale um ingresso para os finais de semana na pizzaria do congresso nacional. 

Tuuuuuuu! Tempo esgotado.  ( O sinal , lembra? )

Observação: No lugar de “sacos” pode ser lido “cuecas”. Entendeu?

Este problema foi adaptado de uma rima infantil do folclore inglês, que pode ser solucionada calculando-se assim:    7⁴ = 7.7.7.7=2401 pintinhos. É muito pintinho!

Veja outra versão da rima em inglês:

As I was going to St. Ives,
I met a man with seven wives;
Every wife had seven sacks,
Every sack had seven cats,
Every cat had seven kits.
Kits, cats, sacks, and wives,
How many were going to St. Ives?

Fonte : http://www.malhatlantica.pt/mathis/problemas/Ives/Ives.htm

Um saco de gatos em Cantuária

Imagem: Caracteriza a cena apresentada na rima em inglês, onde um homem (senhor) encontra uma mulher (senhora) com um saco de gatos. Observe que  ele vai na direção da cidade de St. Ives, e que ela vai na direção de Cantêrbury. Note também que em seu vestido está escrito “Wife” , provavelmente mulher , ou esposa. 

Fonte: Just for the Fun of It, AIMS Foundation

Podemos encontrar muitos problemas matemáticos em versos rimados, e que podem ser utilizados para melhorar nossa interpretação para resolver os mesmos. E este que apresentei acima é um deles, mas claro que se você prestar atenção, a versão em inglês é um pouco diferente, e bastante antiga, pois cada cultura faz suas adaptações necessárias conforme a época e local, e a versão que apresentei é uma adaptação da mesma para o vocabulário tupiniquim, e para nossa época é claro!

[...No uso comum, tupiniquim é metonímia de Brasil ou brasileiro: "plagas tupiniquins", "cantor tupiniquim". E até mesmo "filosofia tupiniquim"...]

Fonte: http://pt.wikipedia.org/wiki/Tupiniquins

Também podemos encontrar outras versões mais antigas que tratam do mesmo assunto, e que podem ser apresentadas de diversas formas. Umas destas é encontrada no Papiro de Rhind. Um documento descoberto, ou melhor, encontrado em 1858, pelo pesquisador escocês Henri Rhind. Estima-se que tal documento, tenha sido escrito por volta de 1650 a.C. Portanto, um achado importantíssimo de quase 4.000 anos. Este documento contém várias informações sobre o sistema de numeração egípcio, conhecimentos de geometria, proporcionalidade, e muitos problemas em versos rimados.

O menino gênio - Carl Friedrich Gauss

      Imagem: Gauss respondendo a pergunta para o seu professor

      Fonte: Revista Galileu. Abril de 2003

          Para saber mais, veja: Gauss – Mais que um matemático. Veja também: O problema 79 do papiro de Rhind (Egipto, século XVI a. C.), no site Malha Atlântica da Professora Dra. Maria João Lagarto. Neste site você encontrará diversas informações históricas a respeito do Papiro de Rhind e outros documentos importantes relacionados à história da matemática.

          Esta é apenas a ponta do Iceberg, ou seja, a introdução à “Potenciação” que foi apresentada neste artigo é apenas uma pequena fração do que podemos aprender com documentos antigos e com a história da matemática. Muitas vezes estamos saturados das aulas cansativas de matemática, e não agüentamos mais tanta fórmula, tanto exercício incompreensível, e por isso, acabamos não enxergando a beleza da arte que está escondida por trás das propriedades, dos problemas, das fórmulas, e do próprio desenvolvimento de um simples exercício matemático ou físico.

A ideia do blog Matemática na Veia é esta. Trazer para você uma matemática que não aprendemos em sala de aula. Uma matemática mais contextualizada com a história, muito mais interessante, e prazerosa. Então, apertem os cintos e peguem suas bóias que “a viagem” vai começar. 

IR PARA O CONTEÚDO  POTENCIAÇÃO

Tópicos do conteúdo:

Observação: Os tópicos 3 e 4 ainda não estão disponíveis no blog, mas os arquivos podem ser enviados por e-mail.  Caso necessário, peça o seu.

1 - Potenciação:Histórias e Rimas 
2 - Potência de expoente natural: Introdução.
3 - Potência de expoente inteiro.
4 - Potências de números Racionais,Irracionais e Reais.   

DOWNLOAD: Espere 60 segundos e clique em baixar . 

Exercícios básicos de potências de números naturais com gabaritos 

Conteúdo deste artigo em formato PDF (Acrobat Reader)

PRÓXIMO TÓPICO: Potência com expoente inteiro

Por enquanto ficaremos por aqui. No próximo artigo vamos descobrir algumas aplicações que envolvem as propriedades do triângulo Aritmético. 

Se você é aluno, professor, ou simplesmente um apaixonado pela matemática, e gostaria de cooperar com dicas, indicar algum blog legal de matemática, ou que seja relacionado à educação, programas legais que conhece, artigos, trabalhos de escola. Mande um e-mail para caco36@ibest.com.br,ou comente aqui mesmo. Agradeço sua cooperação, comentários, dicas, críticas e  sugestões.

Este artigo está em constante atualização, portanto assine o FEED do blog para receber as atualizações gratuitamente.

Share on Google Plus

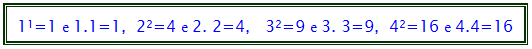
Sobre a Autor:

Antonio Blogueiro desde 2007, gaúcho, gosta muito de ler, e é totalmente viciado em internet. Comecei blogar em 2005, e criei o Matemática na Veia no inicio de 2007. Sou formado em licenciatura Plena em Matemática pela UFPEL. Servidor Público,e fanático pela Web.