O Stomachion de Arquimedes

[♀]Matemática na Veia 2007-2016 O Blog do Estudante Inteligente

Relatos de erros e correções em relação ao português serão bem vindos e podem ser esclarecidos através do RH - Sugestões e Reclamações.

O STOMACHION DE ARQUIMEDES

A invenção de um dos mais antigos, quebra-cabeças geométrico que se conhece é atribuído a Arquimedes, sábio grego que viveu em Siracusa, Sicília, no séc. III a.C.

Esse quebra-cabeça é chamado Stomachion embora não se saiba o significado preciso desta palavra [tem a mesma raiz que a palavra grega para estômago]. A informação sobre este quebra-cabeça chegou-nos através de dois manuscritos muito incompletos [copiados de manuscritos anteriores que se perderam], mas que permitem construí-lo e observar algumas das suas características. Parece que Arquimedes fez um estudo bastante completo do quebra-cabeças, mas esse estudo não sobreviveu aos muitos séculos de guerras, pilhagens, destruições e incompreensão pelos estudos literários e científicos. O Stomachion é constituído por um conjunto de 14 peças planas [originalmente em marfim] de várias formas poligonais com duas características fundamentais: - podem unir-se de modo a formar um quadrado; - a área de cada peça é comensurável com a área do quadrado anterior. O que significa comensurável? Significa que o quociente entre a área de cada peça e a área do quadrado total é um número racional.

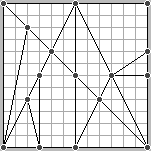
É muito fácil construir o quebra-cabeça, se partirmos de um quadrado de lado igual a 12 unidades. Começamos por traçar o quadrado sobre uma quadrícula de 12 por 12 [se usarmos papel quadriculado; teremos a tarefa muito simplificada]. Em seguida marcamos os pontos indicados na figura e unimos esses pontos. Obtivemos 14 figuras e essas são as figuras que constituem o Stomachion .

A determinação da área de cada figura é fácil se atendermos ao seguinte resultado conhecido como Teorema de Pick:

"A área de uma figura cujos vértices são vértices de uma quadrícula regular (geoplano) é igual ao número de vértices da quadrícula que se encontram no interior da figura mais metade do número de vértices que se encontram sobre a linha limite da figura a que se retira uma unidade"

Este teorema foi descoberto pela primeira vez pelo matemático Georg Alexander Pick em 1899; Pick nasceu em Viena de Áustria em 1859 e morreu durante a II Grande Guerra em 1943 no campo de concentração de Theresienstadt. O teorema de Pick só é válido para figuras simples, isto é para figuras em que os lados não se intersectem a não ser, eventualmente, nos vértices. O teorema é usado, por exemplo, na indústria florestal, para determinar a área de uma região em função do número de árvores [regularmente espaçadas].

Usando este teorema é fácil provar que no Stomachion há 2 peças de área 3, 4 peças de área 6, 1 peça de área 9, 5 peças de área 12, 1 peças de área 21 e uma peça de área 24. Como a área do quadrado formado por todas as peças é 144, a razão entre a área de cada figura e a área do quadrado é, respectivamente, 1/48, 1/24, 1/16, 1/12, 7/48 e 1/6. Na literatura antiga aparecem várias referências ao Stomachion . Marius Victorinus (séc IV) e Atilius Fortunatus [séc VI] chamam-lhe loculus Archimedius [caixa de Arquimedes]. Num manuscrito do poeta e estadista romano Ausonius [séc IV] o Stomachion é comparado a uma forma de poesia em que várias métricas são misturadas. Nesse manuscrito aparece a seguinte forma que se pode dar às peças do Stomachion e que aparenta ser um elefante:

Vários problemas interessantes se podem associar às peças do Stomachion , além de procurar outras figuras sugestivas que se possam formar com as suas peças. Por exemplo: “Agrupar as peças do Stomachion de modo que as áreas [divididas pelo factor três] dos novos fragmentos obtidos sejam representadas por: 1- três números inteiros iguais”.

2- três números inteiros consecutivos

3- “pelos oito primeiros números inteiros, e pelo número 12.”.

[CONVERTED BY MYRMIDON] Convertido com:

Myrmidon: turns any Mac file into a Web page with a single click

Myrmidon info: http://www.terrymorse.com/

Disponível em:

http://www.mat.uc.pt/

Em breve mais atualizações, aguarde.

Se você quer cooperar com dicas, programas, artigos; fique a vontade, e mande um e-mail para caco36@ibest.com.br ,ou comente aqui mesmo, por enquanto ficamos por aqui, Agradeço antecipadamente, comentários, dicas, criticas e sugestões.

Observação: 

- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.

- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .

Assine aqui, o Feed do Matemática Na Veia , e fique por dentro das novidades do blog.

Share on Google Plus

Sobre a Autor:

Antonio Blogueiro desde 2007, gaúcho, gosta muito de ler, e é totalmente viciado em internet. Comecei blogar em 2005, e criei o Matemática na Veia no inicio de 2007. Sou formado em licenciatura Plena em Matemática pela UFPEL. Servidor Público,e fanático pela Web.